eqn: Formatting Equations in groff

August 8, 2023

I have written in the past about groff, a modern implementation of troff/nroff, an old-school, lightweight LaTex alternative. The underlying typesetting system used is incredibly powerful, but is also ugly and difficult to work with. Because of this, most groff documents are written using a combination of macro packages and pre-processing programs, to provide a more convenient interface for specifying document formatting.

Lately, I have taken a special interest in pre-processors. Many take the form of so-called "little languages", simple domain specific languages (DSL) that are designed and optimized for a particular purpose, such as describing diagrams or tables. The pre-processor converts from this DSL into the underlying typesetting language before groff is run.

One such pre-processor is eqn(1). It is designed for describing equations, but has some formatting options that are useful in other contexts as well. At its heart, eqnconsists of a simple language for describing text layout and alignment, and a few built-in definitions for Unicode characters commonly used in equations.

eqn is quite different from the mathematical language used in LaTex, although the two systems are designed to accomplish the same basic task. eqn is small, simple, and internally consistent. It is designed without any special keyword delimiters (like the backslash in LaTex); instead it tokenizes the input on white-space and interprets each token as a potential keyword. The keywords and syntax are chosen to resemble the way in which an equation is spoken aloud, with a few special features for removing ambiguity. For example, a valid eqn expression might be,

.EQ
sum from i=0 to k 2 sup i - i over sqrt 3
.EN

which will render as,

Σ_{i = 0}^{k} 2^{i} - \frac{i}{\sqrt{3}}

Compiling a Document with `eqn`

Before we start adding equations to our groff documents, we'll need to adjust our document compilation pipeline to call the eqn(1) pre-processor. As a pre-processor, we can manually call it in a pipeline, before we get to groff(1) itself. For example, to compile a document written with the ms macro package to a PDF, we could use the following command,

            eqn -Tpdf mydoc.ms | groff -ms -Tpdf > mydoc.pdf

noting that we need to pass the -Tpdf flag to eqn as well as groff. It's generally easier to use groff alone, though. It provides flags for calling a number of standard pre-processors: -e will run eqn. So we can compile our document with,

groff -ms -e -Tpdf mydoc.ms > mydoc.pdf

Including Equations in a Document

When using groff pre-processors, it is necessary to delimit the portions of the document which the pre-processor should evaluate. For eqn, this is done by using the .EQ and .EN macros. I'll call this pair an equation fence, and its contents an equation block. As an example,

.EQ
2x + 1 = 5
.EN

2 x + 1 = 5

This will render the equation on its own line. You can also render equations directly in sentences, without placing them on their own line. These are called inline equations. To use inline equations, you must first define a pair of delimiters: one that starts an inline equation and one that ends it. This is done with the delim keyword, followed by the starting and ending delimiter. I like to use $ for this purpose, but you can use any symbol you like, such as @.

.EQ
delim @@
.EN

You need to place this physically before any attempts to add an inline equation to the document; I tend to place it at the very top. Following these lines, you can add an inline equation like so: @2x + 1 = 5@.

You don't need to use the same symbol as the start and end delimiter, for example,

.EQ
delim @#
.EN

This allows inline equations to be set using: @x2 + 5 = 5#. This might be useful if you want to use an @ in the equation, for example--though you could just use # on both ends in that case, and so I've yet to find a a good reason for using a different starting and ending delimiter.

Basic Concepts

While eqn has a number of keywords built into it, as well as the capacity to define your own, these aren't necessary for the most basic of equations. It has a knowledge of basic mathematical operators, and will automatically add an appropriate amount of space between these and variables/numbers. It will also identify variables and render them in italic text. White-space will be ignored. For example,

.EQ
y=mx+b
.EN

will be rendered like so,

y = m x + b

and

.EQ
y = mx 
+ b
.EN

will result in exactly the same render.

Most of the time, eqn's automatic handling of white-spacing will be appropriate, but it does let you take control and specify your own spacing. The first way to do this is to place text within quotation marks; eqn will render such text verbatim, without any processing. So,

.EQ
"hello there" + 5c - 1 = 9
.EN

will preserve the space in "hello there" and render like so,

h e l l o t h e r e + 5 c - 1 = 9

Note that the text is still set in an italic typeface--we'll see how to set text in roman later.

You can also add spacing using using the ~ and ^ symbols. A ~ represents a full space, and so,

.EQ
hello~there + 5c - 1 = 9
.EN

results in the same formatting as the above example. The ^ is a half-width space, and is useful for adding spacing around binary operators that you define (more on this later). For example, if we wanted to use & as an operator we might write,

.EQ
5^&^1
.EN

which will result in,

5 & 1

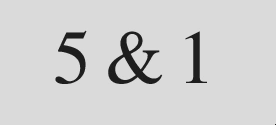
Using a ~ here will result in an awkwardly large amount of space (in my opinion, aesthetic tastes vary), and not using either of characters will result in no spacing between the operator and operand, which also looks awkward.

eqn also supports Greek letters within equations, represented using their name. The lowercase version is specified by using all lowercase letters, and the capital version by capitalizing the first letter. So,

.EQ
pi = 3.14
.EN
.EQ
Delta x = v Delta t
.EN

π = 3.14

Δ x = v Δ t

The use of Greek letters forces us to contend with an important fact of life when using eqn: all tokens must be space delimited. This is something that I mess up continuously. eqn tokenizes its input on words, rather than using a special symbol (like LaTex's backslash) to seperate keywords/commands from text to be rendered. Each word is first checked for any special meaning or definition, and then displayed verbatim if one is not found. One annoying consequence of this that white-space is quite important to how eqn processes input. For example,

.EQ
(pi + 1)
.EN

will not render correctly. eqn will not see pi (a keyword), but rather (pi (not a keyword). The correct way to enter this expression would be,

.EQ
( pi + 1 )
.EN

with extra space around the parenthesis. This even applies to operators, like $pi+1$ or $Delta= 7. Neither of these will render correctly, because there isn't white-space (or ~ or ^) on both sides of the keywords. For someone coming from LaTex, where the input is mostly tokenized by character, this can take a lot of getting used to. [1]

Speaking of parentheses, you can use the left and right keywords to tell eqn to scale the size of the parenthesis with its contents, which will be handy with some of the layout options that we'll discuss later. You can use a single left without a matched right, but not vice versa. You must leave a space between the word and the symbol, like so,

.EQ
left ( x + 1 right )
.EN

You can use these keywords with a variety of separators, such as [ and {. In fact, braces are a reserved symbol in the eqn language, so pairing them with right and left is one of a few techniques for getting the brace symbols to render in your equations.

Keyword Operators

eqn provides keywords for a number of important operators and symbols, although not nearly as many as you may be used to from LaTex. [2] The lack of operators isn't as severe as you may at first think, and is easily remedied (we'll do this in a later section). Most of these are pretty straightforward mappings to a symbol, such as del for $\nabla$ , times for $\times$ , or partial for $\partial$ . But a few involve more complex formatting, such as sum and int for summations and integrals respectively; these symbols will automatically be set in a larger font size. A full list of supported operators is,

Keyword	Symbol	Description	LaTex Equivalent
inter	$\cap$	set intersection	`\cup`
union	$\cup$	set union	`\cap`
prod	$Π$	product	`\prod`
int	$\int$	integral	`\int`
sum	$Σ$	summation	`\sum`
grad	$\nabla$	gradient	`\nabla`
del	$\nabla$	same as grad	`\nabla`
times	$\times$	multiplication cross	`\times`
cdot	$\cdot$	centered dot	`\cdot`
approx	≈	approximately equal to	`\approx`
prime	$'$	prime symbol	`\prime`
partial	$\partial$	partial differential	`\partial`
inf	$\infty$	infinity	`\infty`
>>	$≫$	much greater	`\gg`
<<	$≪$	much less	`\ll`
<-	$\leftarrow$	left arrow	`\leftarrow`
->	$\to$	right arrow	`\rightarrow`
+-	$\pm$	plus or minus	`\pm`
!=	$\neq$	not equal	`\neq`
<=	$\leq$	less than or equal to	`\leq`
>=	$\geq$	greater than or equal to	`\geq`
==	$\equiv$	equivalent	`\equiv`

A number of other common mathematical functions, such as cos, min, and lim all get special treatment as well: eqn will automatically set these in a roman typeface, rather than italic, and add operator spacing before and after them. If you want to force some other text to be roman, use the roman keyword. Note that, unlike \text in LaTex, roman will not escape spaces in its arguments, and so you should put it in quotation marks if you want to preserve spacing, i.e. roman {"you must use quotes"}.

The sqrt keyword is used to specify square roots. This one is a little unique in that it requires braces to indicate the full length of its argument, as the over-line must stretch over everything inside of it. For example,

.EQ
sqrt {2x + 3}
.EN

\sqrt{2 x + 3}

Note that the standard eqn square root operator is widely regarded as ugly when used with large arguments, particularly fractions, such as in this example,

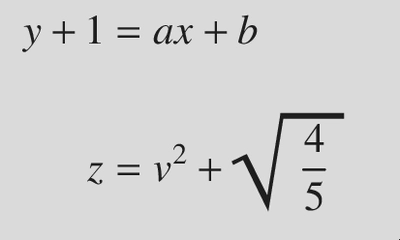
A screenshot of the rendering of the above eqn.

In such cases, the general guidance is to use a fractional power notation instead.

Simple Layout Commands

eqn handles a lot more than just mapping words onto special characters and changing font size and typeface. One of its most useful features is controlling layout: superscripts, subscripts, fractions, summation bounds, etc. These are all very tricky to accomplish in groff without using eqn.

Fractions

First, we'll cover fractions. You write a fraction much like how you might speak it aloud,

.EQ
x over 4
.EN

\frac{x}{4}

where the numerator comes before the over keyword, and the denominator after. If the numerator or denominator include multiple tokens, you can use braces to group them,

.EQ
{ sqrt {x + 4}} over {x - 1}
.EN

\frac{\sqrt{x + 4}}{x - 1}

groff's version of eqn also supports a more compact fraction, using smallover. This is particularly well suited to inline equations, as it requires less vertical space on the page. It can be used anywhere over can.

Text Positioning

eqn provides four keywords for handling text positioning: subscripts, superscripts, and placing text above or below a symbol. This contrasts with Latex, which uses only the _ and ^ operators for positioning, with the interpretation depending upon the context. [3]

The sub and sup operators indicate subscripts and superscripts respectively, and the from and to operators place text below or above a symbol. As an example, you might express a summation as,

.EQ
sum from i=0 to n 3i sup 2 + 1
.EN

Σ_{i = 0}^{n} 3 i^{2} + 1

Keep in mind the tokenization rules here too. If you need multiple tokens in a subscript, summation range, etc., they must be enclosed in braces. And, you must use spaces to separate tokens you don't want included. For example, writing $(3x+y sup 2)$ places the closing parenthesis in the superscript,

(3 x + y^{2)}

which is almost certainly not your intent.

Generally speaking, you can apply these positional adjustments to anything. This is most dramatic in the case of the from and to keywords. Beyond sums and integrals, they are used in limits,

.EQ
lim from {x -> inf} f(x)
.EN

lim_{x \to \infty} f (x)

or for other arbitrary purposes,

.EQ
"hello there" from {"this is under"} to {"this is above"}
.EN

{hello there}_{this is under}^{this is above}

These four keywords provide a great deal of flexibility in text positioning, and aren't tied to particular keywords like sum or lim in the way that LaTex's positioning system is; I find that I prefer eqn's approach. It's true that LaTex can perform these same layout tasks, but it isn't as natural; I use LaTex every day and couldn't tell you offhand how to recreate the previous example.

Complex Layout Commands

eqn provides more complex layout features as well to support equations that span multiple lines. These include using mark and lineup to align text across multiple equation blocks, using tab-stops to place multiple alignment markers (like & in a LaTex align environment, but with more control) or using matrix to specify neatly formatted tables of values. For my purposes, I have barely ever used any of these, though. The layout feature that I use the most are piles.

Piles

The pile (and also lpile and rpile for the left and right aligned versions, respectively) keyword is used to stack multiple expressions on top of each other. The syntax for a pile is quite simple,

.EQ
pile {
    { first line } above 
    { second line } above 
    { third line } above
    ....
    { last line}
}
.EN

with each line being enclosed in braces (if it has more than one token, anyway) and the above keyword being used as a delimiter between lines. in practice, I usually use the left aligned version, lpile. pile is center-aligned, which I feel tends to look weird.

I most recently used a pile in a homework assignment answer key to state a linear program (an optimization problem subject to a set of linear constraints). An example of this is,

.EQ
lpile {
    { max left { 2x sub 1 - x sub 2 + x sub 3 right }
        roman " subject to" } above
    { x sub 1 >= 3 } above
    { x sub 1 + x sub 2 <= 10 } above
    { x sub 2 >= 0 } above
    { x sub 3 <= 4 } above
    { x sub 3 >= 1 }
}
.EN

Piles are also useful for defining piecewise functions. I can never remember how to do this in LaTex. In eqn, it's easy,

.EQ
    f(x) = left { lpile {
        { x sup 2 ,~~~x >= 0 } above
        { 0, ~~~~ x < 0 } 
    }
.EN

Matrices

The next complex formatting command I want to talk about is matrix, for laying out matrices. Matrices build on piles, using the same above keyword to specify rows, but adding a col (also rcol, lcol) keyword as a column delimiter. Note that, the difference between these three columns is in text alignment, not column position. You can have more than three columns.

Matrices are defined in column-major form. The basic syntax is,

.EQ
matrix {
    col { 
        { row 1 } above
        { row 2 } above
        ...
        {row n}
    }
 
    col {
        { row 1 } above
        { row 2 } above
        ...
        {row n}
    }
 
    ...
}
.EN

So you can write a five by five identity matrix ( $I_{5}$ ) using,

.EQ
    matrix {
        col {
            1 above
            0 above
            0 above
            0 above
            0 
        }
        
        col {
            0 above
            1 above
            0 above
            0 above
            0 
        }
        
        col {
            0 above
            0 above
            1 above
            0 above
            0 
        }
        
        col {
            0 above
            0 above
            0 above
            1 above
            0 
        }
        
        col {
            0 above
            0 above
            0 above
            0 above
            1 
        }
    }
.EN

Yes, this is a bit of a wordy representation for a matrix. When you're working with typesetting large matrices, it's probably better to use tbl if possible. But this technique does work well for simple matrices, or for any other simple grid-layouts.

Mark and Lineup

eqn doesn't have a direct analogue to LaTex's align environment, which is used to define multiple equations with matching alignment. However, a simple version of this (with only one alignment point) can be achieved using the mark and lineup keywords. Unlike align, this system spans multiple equation blocks, and so you can align equations that have text in between them too! The general syntax is simple (I hope you're seeing the trend here), use mark to indicate the alignment point, and lineup in future equations to align the following token to the mark, like so

.EQ
y + 1 mark = ax + b
.EN
 
.EQ
z lineup = v sup 2 + sqrt {4 over 5}
.EN

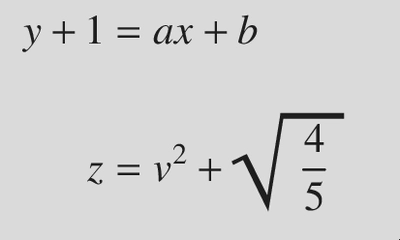
The blank line between the two equation blocks is important here. Otherwise, groff will set them both on the same line.

More alignment using tabs

If you need more than one alignment marker, you can achieve this using tabs.

.EQ
x sub 1 \t
+ x sub 2 \t 
+ 2x sub 3 \t
= y
.EN
 
.EQ
z sub 1 \t 
+ z sub 2 \t
+ 3z sub 3 \t
= u
.EN

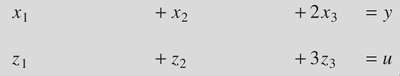
where the \t character represents a tab. You need to use a physical tab character, which may require disabling tab expansion in your editor. The .ta request allows you to specify the custom locations for tabstops if needed, but I haven't tinkered with this enough to get it really figured out.

Custom Operators

One limitation of eqn is that it has a limited set of built-in operators. This is not as big a deal as it may seem, though, because eqn makes it very easy to define your own. eqn uses standard groff character escapes, and so most mathematical symbols you need can be easily accessed this way. You can get a list of the available symbols, and their escape sequences, by reading groff_char(7) in the manual. As an example, the set membership operator, $\in$ , is available as \[mo]. You can write $x \in X$ as,

.EQ
x^\[mo]^X
.EN

These character escapes are a lot to remember though, and I find them and their accompanying spacing characters ugly. Instead, I usually define my own operator keywords and map them to the symbol. You can do this using eqn's define keyword,

.EQ
define in %^\[mo]^%
.EN

The % signs here are an arbitrary delimiter around the value; you can use whatever symbol you want. The purpose of this is to allow you to use quotation marks, braces, etc., within the value of the alias. You can use a delimiter that doesn't conflict with characters you want to in the value itself.

Once eqn processes the above define, any instances of in will be replaced by ^\[mo]^ within equation blocks and inline equations.

.EQ
x in X
.EN

x \in X

There are some mathematical symbols that you still can't get this way, such as blackboard bold or calligraphic letters. These are possible to use with eqn by adding additional fonts, but that is a story for another day.

Conclusion

There's a bit more to using eqn, but not much. This post covers most of what you need to know. That's the benefit of a simple system like this. It isn't as powerful as LaTex's mathematical typesetting, but it's faster to learn and can still do the majority of what LaTex can. I find that I like the syntax of eqn quite a bit more than LaTex, and have been using it, and groff, a fair bit lately to prepare documents for classes that I'm teaching. LaTex is still king when it comes to conference/journal papers, but I'm having a lot of fun with groff for lighter use cases.

References

There are a few important and useful resources for eqn. Here are the ones that I've used to learn it,

The man page: eqn(1). Also, groff_char(7) is very useful.
A Guide to Typesetting Mathematics with GNU eqn
UNIX Text Processing, Chapter 9

[1] Another example of this difference is with superscripts. In LaTex, $x^10$ will render as $x^{1} 0$ , whereas $x sup 10$ in eqn will render as $x^{10}$ . This is all to say that there isn't a clear winner in terms of utility--both approaches to tokenization are annoying in their own way. [back]

[2] Compare with a partial list of LaTex's math symbols, here. [back]

[3] Consider the fact that x_1^2 renders as $x_{1}^{2}$ , but that \sum_1^2 renders as $Σ_{1}^{2}$ ; or as,

Σ_{1}^{2}

depending on if it is used inline or in an equation block. [back]

Compiling a Document with eqn