Linked Lists Revisited

In a previous post I discussed linked lists versus arrays, and ran a number of simple benchmarks with both structures to demonstrate that the common advice of “use linked lists for insertion heavy workloads” doesn’t always pan out in practice. But it got me thinking about possible ways to account for some of the root causes of the poor list performance. So in this post I’ll look at a pair of variations on the structures to further examine their performance.

A Fairer Sorted-Insert Comparison

The first piece of low-hanging fruit from my past post was my comparison of linked list vs. array performance for sorted array insertion. In this benchmark, I performed a binary search on the array to locate the insertion position, but a full scan of the linked list. While I do think that this is a reasonable comparison, I did want to see how much of an effect doing a scan on the array had on the results.

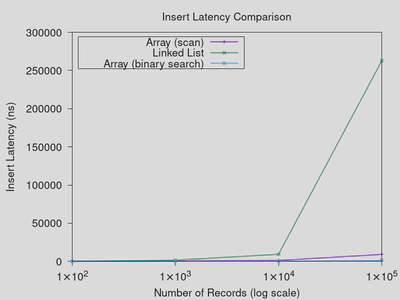
As it turns out, there isn’t a major difference. Unsurprisingly, the cost of insertion into the array is a lot higher with the linear scan, but it still defeats the linked list. This isn’t terribly surprising, we already saw in the last post how a sequential scan of a list is far more expensive than an array because of the array having better spatial locality, and therefore being able to take better advantage of the CPU cache. The binary searchability of the array is significant, but it isn’t necessary to beat a linked list in a drag race.

Improving Node Allocation

I hypothesized that one major bottleneck for linked lists in my insertion benchmarking was memory allocation; each insert requires allocating a new node. First, I used the perf(1) utility to identify hotspots in the code in order to confirm this. The following is a snippet of the perf report, which confirms my suspicion,

  21.58%  a.out    libc.so.6          [.] _int_malloc
  12.36%  a.out    libc.so.6          [.] malloc_consolidate
  11.54%  a.out    libc.so.6          [.] _int_free
   9.32%  a.out    a.out              [.] asl_storage
   7.30%  a.out    libc.so.6          [.] cfree@GLIBC_2.2.5
   6.17%  a.out    libc.so.6          [.] malloc
   4.68%  a.out    a.out              [.] asl_append
   3.71%  a.out    libc.so.6          [.] unlink_chunk.constprop.0
   3.38%  a.out    a.out              [.] main
   1.59%  a.out    [kernel.kallsyms]  [k] 0xffffffffa32947ce
   1.58%  a.out    a.out              [.] asl_destroy
   1.30%  a.out    [kernel.kallsyms]  [k] 0xffffffffa3401237
   0.82%  a.out    [kernel.kallsyms]  [k] 0xffffffffa23b5d30
   0.66%  a.out    [kernel.kallsyms]  [k] 0xffffffffa265c6bd  

With that confirmed, we can define our own allocation system for linked list nodes to alleviate this problem. There is absolutely no reason why we would need to call malloc for each and every node. Instead, we can allocate memory in larger blocks, and then break these blocks apart to form nodes. While I’m not accounting for it here, because I’m not concerned with deletes, this allocator could be given a simple free list to recycle nodes when they are deleted, further improving memory efficiency. Based on this idea, I implemented a new version of the avg_seq data structure which allocates nodes in blocks (of a configurable size). Benchmarking this new structure, compared to the two from my previous post, we find the following insertion performance numbers,

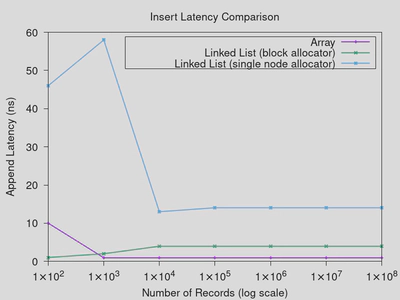
This was run using an allocation batch of 100 nodes per malloc call. Increasing the batch size generally resulted in worse performance for small data sizes (due to large allocations), without substantially changing the picture for larger data sizes, so I stuck with 100. Allocating the nodes in blocks significantly improves the performance of the linked list over allocating single nodes at a time. However, the array-based solution still performs better for insertion than the list-based one for any reasonably sized dataset.

It’s worth noting that this solution does also help with locality, as all of the nodes within a given allocation block are stored sequentially. I considered aligning the nodes to 64 or 128 bytes to reduce the cache advantage from this approach, but the list is losing as it is. Additionally, artificially increasing the node sizes would potentially hurt performance due to requiring larger allocations, which would be difficult to control for. It could be argued that doing this would render the block-allocation implementation non-comparable to the other two.

Conclusion

Despite trying a variety of tweaks to improve the situation, arrays still outperform linked lists in these benchmarks, largely because of cache locality. The obvious solution is to tweak the linked list to use multiple-record node sizes for better locality, however at that point it’s arguable whether we’d still be dealing with a linked list, or some distinct, more complex, data structure. I suspect that this would help a lot, and will take a stab at implementing something like this in the future. But, short of that, it is clear that arrays will typically outperform linked lists in terms of average insertion latency.

If there are any additional tweaks that you think I missed, feel free to shoot me an email with your suggestions. I may test them out and produce another follow up post.