Linked Lists: A Dark Secret

Even when you’d think they’re good… they often aren’t

Douglas Rumbaugh

Feb 28, 2023 8 min read

When talking about data structures, I often like to say that there are two basic ones: arrays and linked lists. These two structures accomplish the same task: storing a sequence of items. But they have their own advantages and disadvantages. Linked lists don’t allow random access, but all for efficient insertion of elements at any point in the list, for example.

However, linked lists have a dark secret. Even in many situations where you would think that they have an advantage–they often don’t. Linked lists will consistently perform worse than you’d expect.

Let’s start with a simple example of a situation where you would think that a linked-list would be better. We’ll implement a data structure called avg_seq which supports two operations: append(float) and average(). The append operation takes an input number (we’ll use floats) and sticks it on the end of the backing structure. The average operation will will iterate over the sequence and calculate the average.

We’ll implement two versions of this structure, one with an array as the backing type, and the other with a linked list. We will then measure the single-threaded throughput of both append and average and compare. We will also compare the storage overhead of the backing structure to see which is more space efficient.

Array-based Structure

We’ll start with the array based structure. More specifically, we’ll need to implement a dynamic array–an array that automatically resizes as needed to support the insertion of new elements. We’ll keep it simple and double the size of the backing array each time it grows. We will also leave off any error checking for simplicity. Do as I say, not as I do: always check the output of malloc/calloc/realloc/etc.

// avg_seq_array.h
#ifndef H_ASA
#define H_ASA
#define ASA_INIT_SIZE 10

#include <stdlib.h>

typedef struct {
  float *data; // the backing array
  size_t cnt;  // the number of elements in the array
  size_t cap;  // the maximum capacity of the array
} avg_seq_array;


static avg_seq_array *asa_create() {
  avg_seq_array *asa = (avg_seq_array *) malloc(sizeof(avg_seq_array));
  asa->data = (float *) malloc(sizeof(float) * ASA_INIT_SIZE);
  asa->cnt = 0;
  asa->cap = ASA_INIT_SIZE;

  return asa;
}


static void asa_append(avg_seq_array *asa, float x) {
  // if there isn't any room, we need to grow
  if (asa->cnt >= asa->cap) {
    float *tmp = (float *) realloc(asa->data, 2*asa->cap*sizeof(float));
    asa->data = tmp;
    asa->cap = 2*asa->cap;
  }

  asa->data[asa->cnt++] = x;
}


static double asa_average(avg_seq_array *asa) {
  float total = 0;
  for (size_t i=0; i<asa->cnt; i++) {
    total += asa->data[i];
  }

  return total / (double) asa->cnt;
}


static size_t asa_storage(avg_seq_array *asa) {
  return sizeof(avg_seq_array) + asa->cap * sizeof(float);
}


static void asa_destroy(avg_seq_array *asa) {
  free(asa->data);
  free(asa);
}
#endif

Linked-list Based Structure

Next, we’ll implement a linked-list version of the same structure. We will only need a singly-linked list to implement the required API. As with many linked-list based data structures, we really don’t need a type to present the structure itself–only a pointer to the head node. But we’ll create one anyway for clarity.

// avg_seq_list.h
#ifndef H_ASL
#define H_ASL

#include <stdlib.h>

typedef struct node {
  float value;
  struct node *next;
} _node;

typedef struct {
  _node *head;
} avg_seq_list;

static avg_seq_list *asl_create() {
  // use calloc to return zeroed memory--we'll use a NULL
  // head pointer to denote an empty list.
  return (avg_seq_list *) calloc(1, sizeof(avg_seq_list));
}

static void asl_append(avg_seq_list *asl, float x) {
  _node *tmp = (_node *) malloc(sizeof(_node));
  tmp->value = x;
  tmp->next = asl->head;
  asl->head = tmp;
}

static float asl_average(avg_seq_list *asl) {
  float total = 0;
  size_t cnt = 0;
  for (_node *nd=asl->head; nd; nd=nd->next) {
    total += nd->value;
    cnt++;
  }

  return total / (float) cnt;
}

static size_t asl_storage(avg_seq_list *asl) {
  size_t total = 0; // we won't count the asl type in the total
                    // as it isn't really required.
  for (_node *nd=asl->head; nd; nd=nd->next) {
    total += sizeof(*nd);
  }

  return total;
}

static void asl_destroy(avg_seq_list *asl) {
  _node *next;
  _node *head = asl->head;

  while (head) {
    next = head->next;
    free(head);
    head = next;
  }
}
#endif

Comparison

Using std::chrono::high_resolution_clock and a small C++ program (which you can find here), I benchmarked these two different implementations across various data sizes to get a handle on their average insertion latency (how long it takes to add an element), overall structure size, and average calculation latency (how long it takes to walk the structure and calculate an average). These results are as follows. 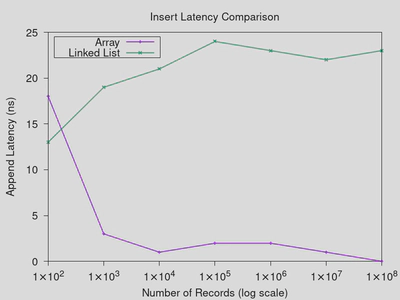Note the log scale in Figure 1’s x-axis. All the other axes are linearly scaled.

The measurement technique that I used had poor precision for small record counts, and so the plots don’t include results for data sizes less than 100.

As you can see, in nearly all cases the linked list performs worse, often by a substantial margin. Even in the insertion latency, where you would think that the cost of reallocating the array compared to the consistent, constant time cost of add a new node to the list, the array dominates for large data sizes.

Insertions into the list (Figure 1) are slower because every single element added to the list requires a memory allocation, which is not free. Note the call to malloc in asl_append. The array-based structure only requires memory allocation when it resizes, which doesn’t happen very often, and so over a large number of insertions the memory allocation costs amortize out to be negligible, whereas the linked list model is effectively a malloc benchmark. Don’t forget to account for the costs of memory allocation–they are not negligible.

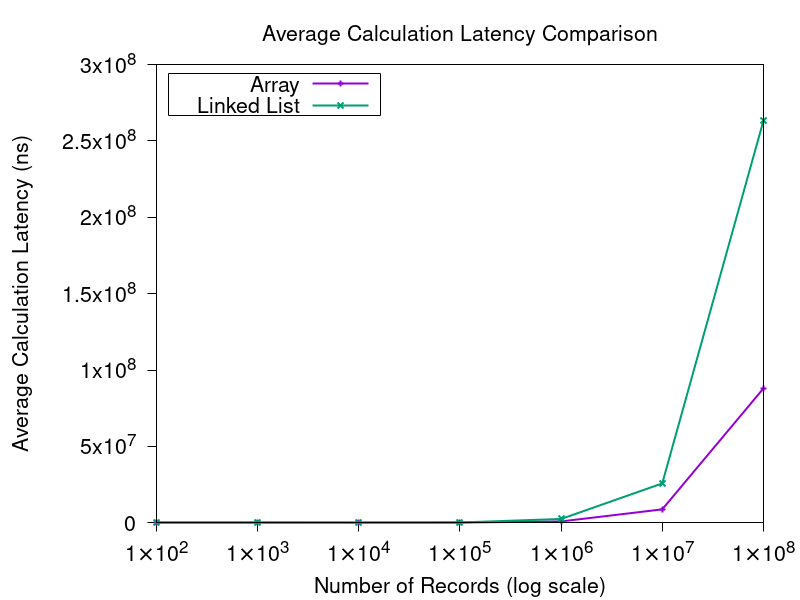
The calculation numbers (Figure 2) are also quite surprising. Here, both operations require the same amount of work: it’s a linear scan of the elements. So you wouldn’t expect the linked-list to be at a disadvantage, as both algorithms examine the same number of elements. However, here the linked-list suffers from memory fragmentation, which ruins its cache performance.

When the CPU needs to access some data in memory, that data is copied into a cache, which is much faster to access. When you read data that is in the cache, the amount of time required for that read to complete is far less. At first glance, this caching doesn’t seem to be useful here, as the sequential scan of the data only touches each element once. However, when a piece of data is copied to the cache, data that is adjacent to it is copied as well. This means that the array, which stores data contiguously, will require far fewer memory access. Each memory access reads 64 bytes (called a cache line) into the cache, and so only 1 in 8 array accesses actually need to go to memory. The linked-list, by contrast, has its nodes scattered all over the place, and so does not benefit from this.

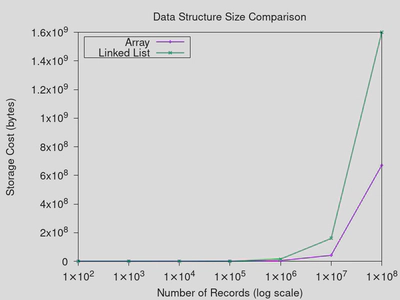
The final plot (Figure 3) is simply to demonstrate that even the storage overhead of the dynamic array, which requires a lot of empty space to ensure decent performance, is less than the overhead of the linked list, which must store pointers as well as data.

Sorted List Insertion

Okay, so in that use case arrays are better. But what about maintaining a sorted list of elements? Surely a linked list, where an element can be inserted anywhere in constant time, will perform better than an array, which will need to both grow, and shift elements, in order to accommodate insertions to random points in the array.

I have prepared implementations for an array-based sorted array, as well as a linked-list based one. I won’t include the code directly in the post for brevity.

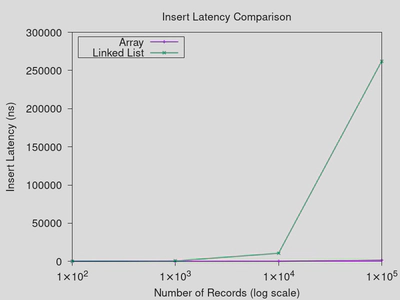
Plot of insertion latency for a sorted list

Even here, the array-based solution dominates. While insertions do require shifting elements around within the array, it is often faster to do this than you might expect using highly-optimized library functions like memmove. The linked-list, on the other hand, requires a linear scan for each and every insert, which is incredibly slow. The array is binary-searchable, and so this scan is avoided. As you can see, the cost of the scan dominates most anything else, even though in principle both the scan and the shifting of array elements have the same algorithmic complexity.

Conclusion

So, where does this leave the humble linked list? Should we banish this structure from our programs entirely? Of course not–they are incredibly useful. Setting aside their convenience, they are also the basis for many more sophisticated data structures that do outperform arrays. They also have more predictable performance. The array implementations above benefit from amortization, which means that the common case is fast, but rarely you’ll hit an array resize or a nasty array shift that will consume a large amount of time. These rare latency spikes can be problematic for certain uses, and are worth being aware of.

In general, I’d say my main point with this is to be aware that reality is more complicated than the “canned” answers that you will often hear. Many people will give well intentioned guidance to the effect of: “linked lists are better in insertion heavy workloads”. Here we have seen two examples where this is simply not the case. Just because something sounds good in theory, doesn’t mean that it will pan out on real hardware. Reality is rarely anywhere near as straightforward as simple dichotomies of “lists good for write, arrays good for read” would have you believe.

Oh, and also, when in doubt, if you can figure out how to solve your problem using an array, it might be worth making the effort to do so. The performance numbers may surprise you. Or maybe they won’t… performance is complicated.