One thing that I have noticed over years spent on the Internet is that there is a seemingly large, and very vocal, group of people who spend a lot of time and energy getting worked up about measurement systems. And, almost universally, their distaste is targeted in one direction: imperial units. Metric good, imperial bad, is the general refrain.

I recently spent a bored evening paging through several anti-imperial/pro-metric videos on YouTube and, in spite seeing a lot of a lot of emotions and non-sequitur arguments, I didn’t find much in the way of actually valid and meaningful argumentation. So I wanted to take a few minutes and write out responses to some of the common arguments (or, in many cases, non-arguments) presented in these videos, from the perspective of someone who, horror of horrors, is rather fond of the imperial system.

Disambiguating Terminology

First things first, we need to establish what we mean by “imperial” and also by “metric” units. The truth of the matter is that these terms mean different things in different contexts, and in different time periods, and it is important to be precise with our language. For example, one interpretation of “imperial” might be the English Engineering system with its truly awful pound-mass (lbm) unit for measuring mass, necessitating an extra conversion factor within equations because its definition is inconsistent with the rest of the system. But that is, of course, not a system I’m going to be defending.

For the purposes of this post, when I use the phrase “imperial system”, “imperial units”, etc., I am actually talking about the more modern British Gravitational System, with its base units of foot-slug-second. And when I talk about metric, I will be referring to the meter-kilogram-second system, also known as SI units.

Neither of those systems have independent volume measurement, using cubic feet and cubic meters as the base volume unit respectively, so I’ll also talk about liters and gallons, and their associated units.

Common Anti-imperial Arguments

Now that we have defined the terms that we are talking about, let’s take a look at some common arguments that I’ve seen crop up within these videos. I’ll do my best to represent them accurately and in good faith. We’ll start with the most obvious one.

Metric Unit Conversions are Easier

One very common argument used in favor of the metric system and against the imperial system is that unit conversions within the system are easier. Metric conversions are done in a fully standardized system, only needing a shifting of the decimal point. Whereas imperial conversions are much more convoluted. A classic example is that $1 \text{ km} = 1000 \text{ m}$, whereas $1 \text{ mi} = 5280 \text{ ft}$.

This is a point that is absolutely true. Performing a conversion from centimeters to kilometers is far easier than from inches to furlongs. You can’t really argue otherwise. However, I would argue that this point is pretty much irrelevant for most practical situations. The fact of the matter is that unit conversions fulfill very different purposes in metric and imperial, and so to compare the relative difficulty of conversion between two metric units, and two imperial units, isn’t particularly valid. Metric unit conversions are used primarily to condense the representation of numbers, and imperial unit conversions are mainly used to ease measurement or calculations.

In the case of metric, a unit conversion is performed by shifting the decimal point around, which changes a prefix on the unit in question. For example, there are 100 centimeters in 1 meter. So 10 meters is equal to 1,000 centimeters. This is a very straightforward and easy process–but, at least in my opinion, it’s largely vacuous.

The reason why I say this is that, effectively, all that this scaling up-and-down of the units accomplishes is reducing the number of insignificant digits that you need to represent with a 0. If you have 1200 meters, you can avoid writing two of those zeroes by instead writing 1.2 kilometers. But, in practice, that’s all that you accomplish.

This is made even less significant by how these unit conversions are actually used in practice. Without going too deeply into the weeds of dimensional analysis, the equations used in science and engineering only work out cleanly when the units associated with all of the physical quantities used as inputs to the equation align. As a simple example, in Newton’s 2nd Law of Motion, $$ \vec{F} = m\vec{a} $$ The force ($\vec{F}$) is conventionally expressed in Newtons. But this only works if mass is in kilograms, and acceleration is in meters per square second. If you were to use a mass in grams, the result would only be in Newtons if you also converted the acceleration to be in millimeters per square second. All of the quantities need to be scaled up or down the same amount–otherwise you’ll get a result in a non-standard set of units for force. This is actually why the CGS system defines its own unit of force, the dyne, for using centimeters and grams together in this equation, and others.

In practice, what this means is that, when working in the SI system to do science or engineering, you rarely use kilometers or milligrams or centimeters. It causes too much of a hassle making sure that all of your units are consistent with each other. Most people simply convert everything into meters and kilograms, and then go from there. And then it is far simpler just to leave the resulting quantities in the base units as well, because scientific notation handles perfectly well the compression of insignificant zeroes, without requiring the next person to need to undo your conversions before using the result in another calculation.

Likewise, it is very rare in real life to convert from feet or yards into miles when using the imperial system. It isn’t as though people actually use these as subdivisions of one another in most cases. You’d never see someone report a distance as “5 miles, 1571 yards, 2 feet, and 9 inches”. You will see people use feet and inches alone like this (and sometimes yards), but never will miles be thrown into the mix. And the conversions for inches, feet, and yards are are easier than the strawman example of feet and miles that is commonly bandied about. They’re still more complex than simply shifting the decimal, like in metric, but for the additional complexity, these conversions actually aid in performing calculations with these units. For example, if you wanted to subdivide a foot into 3 equal parts, it’s much nicer to think in terms of 4 inches than in terms of .33333333333333333333… feet.

So yes: it is true that unit conversions are far easier in metric than they are in imperial. But the commonly provided examples of difficult imperial conversions are, in practice, almost never used, and the commonly used conversions in imperial are relatively simple (though, admittedly, not as simple as metric).

The Imperial System is a Mess

I’m not going to write at length on this one because it seems to me to be largely a non-sequitur. You’ll frequently see this image bandied about as though it proves something,

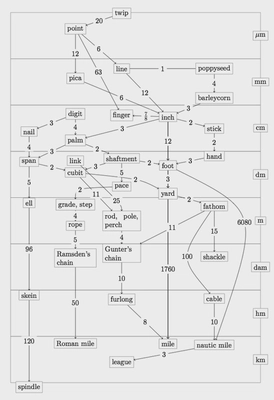
This image shows the relations between many different units of length used in the imperial system, with their conversion factors. And it’s true, as rendered in that figure the system seems very complex compared to metric, which doesn’t even warrant a diagram as the only unit of length relevant there is the meter.

The trouble is that this image is also incredibly misleading. The imperial system is a lot older than the metric system, and has picked up a lot of additional baggage of the years. Most of the units shown on this diagram are either (a) not in use any more, or (b) used in very specific contexts.

Unless you’re doing surveying work or typography, it is likely that the only units that really matter on this chart are inches, feet, yards, and miles.

That said, there are examples of imperial units where this critique is valid. One commonly noted example is the definition of a “barrel”, of which there are several versions used in different contexts. Similarly there is the short and the long ton. But, again, these distinctions arise in very specialized areas. And the barrel situation can be fixed via standardization within the imperial system, without a conversion to metric.

Similar odd units crop up in metric too, like shakes, angstroms, light-years, light-nanoseconds, parsecs, electron-volts, foes, ergs, etc. One might argue that these are obscure, or relevant to very particular scientific domains. To which I would reply that the same can be said of links, cubits, and skeins.

The Mars Climate Orbiter, Air Canada Fueling Incident, and other Such Examples

Another common argument used against imperial are accidents that were caused due to either misconversions, or miscommunications in areas where both metric and imperial units were used concurrently. These are not arguments specifically against imperial. The accidents that occurred were not due to the imperial units themselves, but rather due to environments in which two unit systems were used together. These examples demonstrate that using only a single unit system at a time in a given context is a good idea, but don’t provide any specific condemnation of imperial. The same could have happened at the interface between two metric systems (Like SI and CGS).

Scientific Literacy

One particularly interesting argument that I saw was brought up by Kurtis Baute at around 4:30 in this video. He argues that science is fundamentally about taking measurements–which is absolutely true, and that being able to accurately take a measurement is important to science and scientific literacy, which is also very true. He then goes on to say that the use of imperial units prevents people from knowing “what a meter is” and implies that this prevents them from being able to do science.

Okay, so to be fair I did pick a pretty over-the-top variation of this argument to lay out. Generally speaking, science is done using metric, and so in order to participate in science, one must learn metric. This is true. However, I don’t think that the use of imperial units within the US significantly hurts metric literacy.

For one thing, metric is taught in schools in the US. I certainly learned it, and I’m sure most other Americans did as well. In fact, for a few years I managed a general physical sciences course at a university that I worked at–the sort of base-level exposure course that every first-year student was required to take–and I was consistently surprised by how almost every student was much more comfortable with metric than with imperial. I think that it has to do with the fact that the imperial system relies heavily on fractions, rather than simple decimal shifting, which seems to be a trouble-spot for a lot of students.

As a side note here, I sometimes feel that the metricization of science in high school goes perhaps a little too far. It is not uncommon when judging high school science fairs to see very strange quantities in either experimental procedures, or in results sections. For example, one might see a methods sections including “56.7 grams of baking soda were added to 236.59 milliliters of water” as one of the steps. Why such strange numbers? Because the student in question was doing an experiment in their kitchen, and measured out 2 oz. of baking soda to add to 1 cup of water. But because “SCIENCE MUST BE METRIC!!!!”, instead of reporting the precise measurements that they took on the instruments that they had available, they lose precision and do silly and unnecessary conversions for no good reason. To accurately report the measurements that they took in the form that they took them would result in losing points in judging, because metric is the only acceptable unit system in science.

Convenient “rough” Estimates between Dimensions

Another advantage of the metric system is the convenient conversion between the standard SI volume units, and the non-standard but commonly used volume unit of liters. Specifically, one cubic centimeter is equal to one milliliter. And further, 1 milliliter is roughly equal to 1 gram of water. Yes–this is a rough and somewhat problematic conversion, but it gets brought up a lot.

Taking an example from this video, then, can we easily calculate how much water we can haul in our truck, with a max payload of 1,000 kilograms, $$ 1000 \text{ kg} * \frac{1 \text{ L}}{1 \text{ kg}} = 1000 \text{ L} $$

What he doesn’t mention is that a similar conversion exists in imperial, one pint of water weighs about 1 pound. It isn’t quite as precise as the metric case, but is close enough for practical use (it’s about 4% off). So to do the same problem in imperial units, (using 1 ton instead of 1000 kilograms) $$ 2000 \text{ lbs} * \frac{1 \text{ pt}}{1 \text{ lb}} = 2000 \text{ pt} $$ Now if we wanted the result in gallons, we’d need to divide by 8, which I admit isn’t quite as convenient as shifting a decimal place. But it still isn’t too bad: 250 gallons. The correct answer is 260–which is slightly under 4% higher than the estimate. Not too bad for a stupid, horrible unit system.

In either case–this is very much in the “rough” calculation territory in precise situations, because the density of water is actually a function of temperature and pressure, and so such calculations will always have a margin of error unless these other variables are also accounted for. At which point a thermodynamic table must be consulted, and any illusion of “speedy calculation” goes out the window in both cases.

Metric Units are Fundamental

These days, the metric units have all been defined in terms of universal constants. Thus, these units are fixed to the fundamental nature of the universe in some way.

Of course, these definitions are retroactive. The units had already existed, and were simply tied back to some fundamental constant with a random conversion factor applied to make sure that the defined value matched up with the original one. And, of course, imperial units are defined in terms of metric ones now, and so have just as strong an argument to “fundamentality” as the metric ones do. If you’re going to define a meter with the constant $\frac{1}{299792458}$ relative to a fundamental constant, and a foot with the constant $\frac{1}{913767411984}$ relative to that same fundamental constant, can you really claim one is “more fundamental” than the other? Those are both pretty ugly numbers.

The Imperial System uses Pound for both Mass and Weight

It used to. It doesn’t anymore. The British Gravitational System does away with pound-mass and has the slug as a unit of mass instead. No ugly conversions needed. However, the metric system, in general use, uses the kilogram for both mass and weight. If anything, the imperial system is more accurate to reality here, measuring weight with a unit of force.

Conclusion

After all this, I do want to say that I do like metric units and use them quite regularly. But I also like imperial units, and use them regularly too. I’ll concede that there are definitely situations where metric units are better than imperial (drill, tap, and screw sizing come to mind…). But I get consistently annoyed by the metric elitists bandying about bad arguments for their good system, and so I wanted to address some of those arguments here. Imperial units are not automatically dumb, imprecise, or non-scientific. And you can do perfectly good work no matter which unit system you choose.